Pythagorean Theorem Problems

The problems on this page involve many mathematical relationships. The thing they have in common is that the Pythagorean Theorem is utilized in the solution, but it is not obvious at first glance to use the Pythagorean Theorem. Below is my criteria for problems on this page.

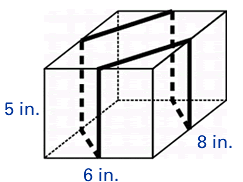
Ribbon Around a Box Problem A rectangular box is tied with a ribbon so that the ribbon crosses the box at the midpoints of its sides. If the box is 8 inches long, 6 inches wide, and 5 inches high, how long is the ribbon? (This problem from Figure This from the NCTM - Challenge #55).

Corner to Corner Stretch Problem What is the length of the shortest string that can stretch from point X to point Y along the outside of the box in the diagram? (The dimensions are in inches.) (This problem from Figure This from the NCTM - Challenge #55).

Balls in a Cone Problem Three balls are placed inside a cone such that each ball is in contact with the edge of the cone and the next ball. If the radii of the balls are 20 cm, 12 cm, and r cm respectively, what is the value of r? (This problem from www.mathschallenge.net.).

Criteria for Problems on This Page

Problems I have selected to put on this page meet the following criteria:

• The problem is a good problem-solving problem.
• It utilizes the Pythagorean Theorem in the solution, but it is not obvious at first glance to use the Pythagorean Theorem.
• The problem involves mathematical (often geometric) properties other than just the Pythagorean Theorem. It is worth noting that the aspect that make many of these problems challenging is not the Pythagorean Theorem.

James R. Olsen, Western Illinois University
E-mail: jr-olsen@wiu.edu
Page last updated: February 12, 2004