Instructional programs from prekindergarten through grade 12 should enable all students to—
|
To meet new challenges in work, school, and life, students will have to adapt and extend whatever mathematics they know. Doing so effectively lies at the heart of problem solving. A problem-solving disposition includes the confidence and willingness to take on new and difficult tasks. Successful problem solvers are resourceful, seeking out information to help solve problems and making effective use of what they know. Their knowledge of strategies gives them options. If the first approach to a problem fails, they can consider a second or a third. If those approaches fail, they know how to reconsider the problem, break it down, and look at it from different perspectives—all of which can help them understand the problem better or make progress toward its solution. Part of being a good problem solver is being a good planner, but good problem solvers do not adhere blindly to plans. Instead, they monitor progress and consider and make adjustments when things are not going as well as they should (Schoenfeld 1985).
In high school, students' repertoires of problem-solving strategies expand significantly because students are capable of employing more-complex methods and their abilities to reflect on their knowledge and act accordingly have grown. Thus, students should emerge from high school with the disposition, knowledge, and strategies to deal with the new challenges they will encounter.
As in the earlier grades, problems and problem solving play an essential role in students' learning of mathematical content and in helping students make connections across mathematical content areas. Much of school mathematics can be seen as the codification of answers to sets of interesting problems. Accordingly, much of the mathematics that students encounter can be introduced by posing interesting problems on which students can make legitimate progress. (See, for example, the use of such an example in Mr. Robinson's class, as described in the "Connections" section of this chapter.) Approaching the content in this way does more than motivate students. It reveals mathematics as a sense-making discipline rather than one in which rules for working exercises are given by the teacher to be memorized and used by students.
Problem solving plays a dual role in the high school curriculum. On the one hand, solving problems that have been strategically chosen and carefully sequenced is a fundamental vehicle for learning mathematical content (see the "counting rectangles" problem later in this section). In addition to carefully designing problems, teachers should seize unexpected opportunities (see the discussion of Ms. Rodriguez's class later in this section) to use problems to engage students in important mathematical ideas and to develop a deep understanding of those ideas through such engagement. Most mathematical concepts or generalizations can be effectively introduced using a problem situation that helps students see important aspects of the idea to be generalized. For example, rather than begin the consideration of the volume of a sphere by reminding students of the formula or technique for computing the volume, a teacher might begin by posing a question such as "How might you find the volume of a sphere whose radius is ten centimeters?" As students consider possible approaches, they can come to appreciate the difficulties inherent in what appears to be an easy question. In other instances, their proposed solutions may either directly lead to the desired conclusion or serve as a springboard to class discussions of the idea.
On the other hand, a major goal of high school mathematics is to equip students with knowledge and tools that enable them to formulate, approach, and solve problems beyond those that they have studied. High school students should have significant opportunities to develop a broad repertoire of problem-solving (or heuristic) strategies. They should have opportunities to formulate and refine problems because problems that occur in real settings do not often arrive neatly packaged. Students need experience in identifying problems and articulating them clearly enough to determine when they have arrived at solutions. The curriculum should include problems for which students know the goal to be achieved but for which they need to specify—or perhaps gather from other sources—the kinds of information needed to achieve it. Recall, for example, the "track lighting" problem discussed in the "Geometry" section of this chapter. In addressing the problem, students would need to know about the geometry of the floor plan, about the structure and height of the ceiling, about the positioning of the "customer area," and about the areas that should receive priority lighting.
The following problem serves multiple purposes. It gives students an opportunity to build their content knowledge during the problem-solving process, to learn or practice some heuristic strategies, and to make connections among various ways of thinking about the same mathematical content. It might be posed during a unit on combinatorics or as part of an ongoing series of problems that are given out of context so that students have to determine the relevant approaches for themselves.
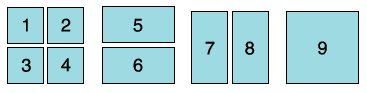
How many rectangles are there on a standard 8x8 checkerboard? Count only those rectangles (including squares) whose sides lie on grid lines. For example, there are nine rectangles on a 22 board, as shown in figure 7.27.

Fig. 7.27. Rectangles on a 2x2 "checkerboard"
There are numerous ways to approach and solve this problem. Students should be given significant latitude to explore it rather than be led » directly to the solution method or methods that the teacher has in mind. With planning, a teacher can use such explorations to develop interesting mathematics and to make connections that might otherwise be overlooked.
Often students begin this problem by trying to count the number of rectangles directly, but it is hard to keep track of which rectangles have been counted, so they usually lose count. This situation presents an opportunity to discuss the need to be systematic—to find an approach that will identify all rectangles on the board and count each only once.
Typically, some students continue to count while others look for alternatives. For problems such as this one, it is often useful to consider the heuristic strategy "try an easier related problem." But which related problem should they try, and what is to be learned from it? Some students will want to count rectangles on the 3x3 and 4x4 boards, looking for patterns. The results for the 1x1, 2x2, 3x3, and 4x4 boards are 1, 9, 36, and 100, respectively. This result suggests that the number of rectangles on an nxn grid is (1 + 2 + ... + n)² —a very nice observation that leaves unanswered the question of why the sum should be what it seems to be. Some students might focus on developing a systematic way to count the rectangles on the smaller grids, and then return to the 8x8 grid to apply what they have learned. Others will try to show that the generalization holds by using the result from the nn square as a stepping-stone to counting the rectangles in the (n + 1)x(n + 1) square. They discover that it is difficult and may need to turn their attention elsewhere. An important lesson about problem solving is that not all approaches work and that after consideration, some need to be abandoned.
The heuristic "trying an easier related problem" can be implemented in other ways in solving this problem. Instead of working with an nn board, for example, some students may look for ways to count rectangles on a 1x8 board. That the 1x8 board has 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 different subrectangles can be shown in a number of ways, and students can compare notes on how efficient or compelling their methods are. When they work on the 2x8 board, they may notice that the pattern of rectangles found in the 1x8 example can be found in the top row, in the second row, and extending across both rows. This strategy has a natural extension to 3x8 boards, and so on. Students should reflect on the value of strategies that can easily be generalized to other examples. Teachers can ask them to talk about and demonstrate that their strategy works in all such instances and convince others of its validity. As the students do so, they are exploring patterns systematically and verifying algebraically that the patterns hold.
Simple questions such as "What determines a rectangle?"—a version of Pólya's (1957) heuristic strategy "look at the unknown," tailored to this situation—can help students reformulate the problem. Some students may recognize that it is possible to characterize a rectangle on a » grid by specifying two opposite corners. They could then count the number of rectangles that have a fixed upper left corner on the 8x8 grid as follows: Pick any corner on the grid. If there are m grid lines below that corner and n grid lines to the right of it, the number of rectangles on the grid with that point as an upper left corner is mxn. The number of rectangles can then be indicated, as shown in figure 7.28, where the product written in each square of the grid is the number of rectangles on the whole grid that have the same upper left corner as the square. The task becomes to add the 64 numbers in the grid. The first column sums to 8(8 + 7 + ... + 1), the second column to 7(8 + 7 + ... + 1), and so on. Hence the sum of the columns is (8 + 7 + ... + 1) (8 + 7 + ... + 1) = (8 + 7 + ... + 1)2. This result confirms the conjecture that some students had made earlier, when they examined the 1x1, 2x2, 3x3, and 4x4 grids, and presents an opportunity to see how one approach can shed light on a result obtained by another method. Also, once the pattern is apparent, the students should be encouraged to abstract and represent their results for more-general cases. They should, for instance, be able to conjecture that the number of rectangles on an nm board is (1 + 2 + ... + n)(1 + 2 + ... + m). From other work they might have done adding sequences of consecutive integers, they should be able to represent this as [(n)(n + 1)(m)(m + 1)/4].
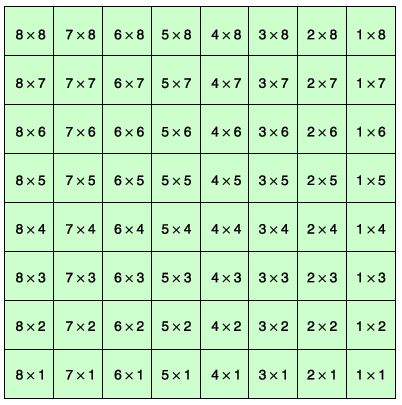
Fig. 7.28. The number of rectangles in an 8x8 grid
Other heuristics may also prove useful. Some students may notice that each rectangle in the 8x8 grid is determined by the lines on which its top and bottom borders lie (there are C(9,2) choices) and the lines on which its left and right borders lie (also C(9,2) choices). So there are C(9,2) x C(9,2) rectangles in the 8x8 grid. This approach can be generalized to show that there are C(n+1,2) C(m+1,2) rectangles in an nxm grid. Thus, this problem provides students with an opportunity to review counting techniques and show their power, as well as to use their prior knowledge in other approaches to solving the problem. Moreover, just as the class has not » finished when students have found one solution—the variety of solutions is important—it has not finished when a variety of solutions have been found. A teacher and a class with a problem-solving disposition will be quick to formulate interesting extensions such as, What would an analogous three-dimensional problem look like?
In addition to using carefully chosen problems with particular curricular purposes in mind, teachers with problem-solving dispositions can take advantage of events that occur in the classroom to promote further understanding through problem solving. Such an opportunity arises in the following story, based on Zbiek and Glass (forthcoming):
Ms. Rodriguez's class was studying classes of functions. The focus of the lesson was on exploring the properties of the graphs of quadratic functions. To ease the students into the use of dynamic graphing technology, the lesson began with parametric explorations of a more familiar class of functions, linear functions of the form f(x) = mx + b. Ms. Rodriguez introduced students to the day's goal:
Ms. R.: Today, we will learn about a new family of functions called quadratic functions. But first, you will need to become familiar with a new type of computer representation. So we will begin by exploring a familiar family, f(x) = mx + b. You will be using a computer sketch with sliders to change the values of m and b. I think you'll like using the sliders—they'll save you a lot of work and let you concentrate on big ideas.
The computer software enabled the students to change the value of m or the value of b and observe the effects of these changes on the graph of f(x) = mx + b. Ms. Rodriguez demonstrated the use of the top slider to control the value of m and the bottom slider to control the value of b (see fig. 7.29 for a view of the slider screen). She then handed out a worksheet to structure the students' activities.
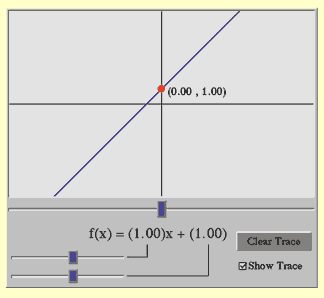
Fig. 7.29. A slider screen
E-Example 7.5
As often happens, some students were exploring the graphing software without following the instructions on the teacher's worksheet. Shelly was one of those students. Soon she was calling for Ms. Rodriguez's attention:
Shelly: Ms. R., Ms. R.! I found something really awesome!
Ms. R.: That's great, Shelly. But don't tell others what you've seen yet. I want the others to have a chance to make their own discoveries. Please keep track of your work for when we compare notes.
As she approached Shelly's desk, Ms. Rodriguez expected the trace function on Shelly's computer to show a set of parallel lines (if Shelly had used the slider for b )or a set of lines that pass through the same point on the y-axis (if Shelly had used the slider for m). What she saw was different (see fig. 7.30). Ms. Rodriguez was puzzled.
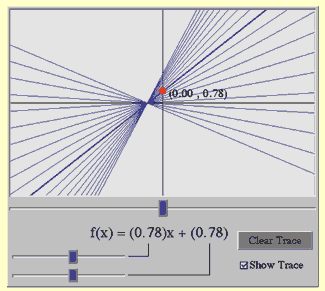
Fig. 7.30. Shelly's screen
Ms. R.: Shelly, could you show me how you got the computer screen to that point?
Shelly: I don't really know, but for some reason, when I moved m, b also moved.
Ms. R.: Can you do it again?
Shelly demonstrated, clicking on m and b in such a way that both sliders moved at the same time and rate. Since the m and b scales were the same, as she moved m, b moved the same amount.
Ms. R.: What's the really awesome thing you are seeing?
Shelly: Look! They all intersect at the same point.
Ms. R.: That is really interesting!
Ms. Rodriguez found this observation intriguing and decided that exploring the situation might lead to some interesting insights. She asked Shelly to show the class how she created the pattern. Soon Michael, intrigued by Shelly's result, tried her technique on another function, with the result shown in figure 7.31.
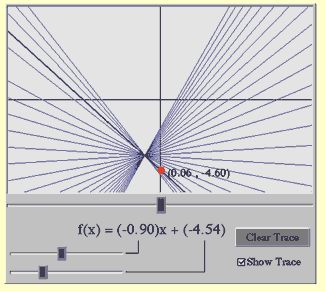
Fig. 7.31. Michael's screen
Michael: Look at what happened! I got the same thing as Shelly, but I started with a different function.
At Ms. Rodriguez's request, Michael demonstrated his finding for the class.
Ms. R.: Tell us what you mean when you say you "got the same thing."
Michael: All my lines crossed at one point.
Jerod: I tried a different one, and mine crossed at one point!
Ms. Rodriguez saw this development as an opportunity for group problem solving and knew that she could entice her students with a challenge. She asked, "Can anyone come up with a similar picture for another linear function?" The room buzzed with activity as students tried Shelly's technique. Some students helped one another learn the technique while Ms. Rodriguez helped others. Every time the students applied Shelly's technique to a linear function, their set of equations passed through one point. As the students compared their results, they began to notice that the points of intersection always had the x-value –1, a fact that rippled rapidly through the » classroom. Ms. Rodriguez brought the class to a close with a discussion of what had been found. The class was sure that Shelly's method produced the same result for all linear functions, and the students had mixed opinions about whether it would work for other functions. A student formulated a statement of the class's conjecture and wrote it on the board as follows:
Applying Shelly's technique to a linear function results in a set of linear functions, all of which pass through the same point. The point of intersection has an x-value of –1.
The next day, Ms. Rodriguez began the class by asking each student to choose a linear function and apply Shelly's technique to it. She told the students that each person would be responsible for showing why Shelly's method did or did not work for his or her function. As the students worked on symbolizing what they had done, questions arose such as, What should I write down? I know I want to show that they all intersect in the same place, but how do I show that? Ms. Rodriguez suggested that students work together in small groups. At some point, each group realized that the solution involved finding the point of intersection of the graphs of two equations—the one they started with and a second one. Karen produced the following argument:
My equation was y = 3x + 5. I moved the sliders about two units to the right. The equation for the new line had m and b two units bigger than the original. So the new line was y = 5x + 7. I found the intersection of those two lines and got 2x + 2 = 0, so the intersection is at x = –1 and y = 2. [Karen wrote the following on the chalkboard.]
3x + 5 = 5x + 7
0 = 2x + 2
-2 = 2x
-1 = x
Pao announced excitedly that Karen's approach worked even for an equation as
complicated as y = –3.23x + 4.577. After most of the students had found
that their equations intersect at a point with an x-value of –1, Ms.
Rodriguez led the class in a discussion of exactly what they knew. Mike argued
that since they had chosen their equations randomly, the result must be true
in general. Pete said that even though they had looked at several equations,
their results were not sufficient to prove the conjecture for every equation.
Pat added that they also hadn't tried every possible movement of m.
The discussion of this problem continued until the class generated a general proof. With Ms. Rodriguez's guidance, the students worked to represent the result of the simultaneous slider shift of a linear function written in the form y = mx + b as y = (m + k)x + (b + k). The students determined the point of intersection by solving the system of equations:
y = mx + b
y = (m + k)x + (b + k)
They then confirmed that every equation of the form y = (m + k)x +
(b + k) passes through the point (–1, b – m).
Ms. Rodriguez may well have felt very satisfied at the end of this episode,
since her class had had an opportunity to explore a striking graphical pattern
observed by a student. The exploration had included considering whether it
would always work and if so, why. Pursuing the answer to that question helped
her students see the linkage between algebraic and graphical representations
of functions and understand how algebraic arguments can be used to establish
the truth of a mathematical conjecture. It gave them an opportunity to review
and apply previously learned knowledge of solving systems of equations. She
will have to revise her instructional plan for the coming weeks. However,
this experience has helped reinforce her students' dispositions toward posing
and solving problems as well as their algebraic fluency. Indeed, the situation
may have helped her students realize that mathematical situations can be
interesting and worthy of exploration. Thus problem posing and problem solving
led to a deeper understanding of both content and process.
As Halmos (1980) writes, problem solving is the "heart
of mathematics." Successful
problem solving requires knowledge of mathematical content, knowledge of problem-solving
strategies, effective self-monitoring, and a productive disposition to pose
and solve problems. Teaching problem solving requires even more of teachers,
since they must be able to foster such knowledge and attitudes in their students.
A significant part of a teacher's responsibility consists of planning problems
that will give students the opportunity to learn important content through
their explorations of the problems and to learn and practice a wide range of
heuristic strategies. The teacher must be courageous, for even well-planned
lessons can veer into uncharted territory. Students may make novel suggestions
as they try to solve problems; they may make observations that give rise to
new conjectures or explorations; they may suggest generalizations whose validity
may be unknown to the teacher. Teachers must exercise judgment in deciding
what responses to pursue and recognize the potential for both productive learning
and improved attitudes when students generate new ideas, but they must also
acknowledge that not all responses lead to fruitful discussions and that time
constraints do not allow them to pursue every interesting idea. It is the teacher's
job to make the tough calls. The teacher must also be reflective in order to
create an environment in which students are inclined to reflect on their work
as they engage in it (Thompson 1992). In short, teaching is itself a problem-solving
activity. Effective teachers of problem solving must themselves have the knowledge
and dispositions of effective problem solvers.
Copyright © 2000-2004 by the National Council of Teachers of Mathematics.
Page note: This page prepared by Jim
Olsen of
Western Illinois University for use by students
enrolled in his courses. Errors on this page should be reported to Jim
Olsen.