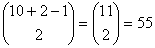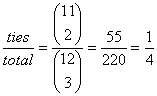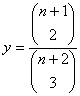Math 355 - Combinatorics
This page is for Math 355 students at Western Illinois University.
Renee and Eric made physical models of the balls dropping through Pascal's
Triangle. For a computer simulation of the balls dropping see Ryan's program
at http://student.wiu.edu/RJ-Gerry/math/pascal.html.
The program runs nicely.
Check out Probability
Plaza Interactive - Four of the five topics are central to our course.
The topics are:
- Combinations and Permutations Calculator
- Pascal's Triangle Row Generator
- (3M Calculator just calculates mean, median, and mode)
- Bell Curve Simulation - ala Renee, Eric, and Ryan's projects - NOTE:
you have to click the
arrow at the top
of the triangular grid to make it work!
- Block-Walking Calculator
New related problems have been added below in a Word
document. I'm continuing to append to the document.
Try solving these problems
- There are 14 businessmen in a room. Each person exchanges business cards
with everyone else once. How many total exchanges are there?
- 19 math students are reviewing for a test. They are separated out amoung
4 rooms in a school such that there are 7 students in Room A, 5 in Room B,
4 in Room C, and 3 in Room D. Every student is given a sheet of paper with
19 review questions on it. Each student is also given 1 answer to one of the
problems so that all of the answers are given out. Each student is to get
all the answers to the problems by exchanging answers one-by-one first with
all of the students in the same room. When that is done, all of the students
gather in Room E to get all the answers from the students previously not in
the same room in the same fashion as before. After each student gets all the
answers, they separte back out into the 4 rooms as before. Once there, they
go around one-by-one and check with everyone else in their room to make sure
everyone got the correct answers to each question. How many total meetings
are there between answer exchanges and checking for the right answers? (Hint:
you first have to meet with every other student once to get the answers.
Then you meet with each person in your group to check the answers. How many
meetings are there?)
- Determine how many ways 30 soldiers can be selected from four squads filled
with privates, corporals, sergeants, and specialists. (Each squad is filled
with only one type of soldier.)
- Determine how many ways can you select 10 writing utensils from the store.
There are blue pens, black pens, and pencils. There is an unlimited supply
of each.
- Consider the following pseudo code below.
for i := 1 to n do
for j := 1 to i do
for k := 1 to j do
print "hello"
end
end
end
a) Assuming that variable "n" in the code above is set to 20,
how many times will the print statement be executed?
b) Derive a general formula for the number of times the print statement
is executed in terms of n.
- A small company of 10 employees is choosing a new health insurance plan.
Three of the company's employees have done research and have each chosen a
separate health insurance plan. The companies president would like to use
"Approval voting" to allow her employees to choose from one of the
three health insurance plan. Approval voting works by allowing voters to vote
for as many options as they wish. For example, an employee could vote for
his or her two favorite plans, but not vote for the third. A valid vote in
approval voting would be for a voter to vote for all three, two, one, or none
of the possible insurance plans. There is no either - or situation in approval
voting. It is assumed that the three employees who researched and found a
plan will vote for only that plan (that is, every plan will receive at least
one vote).
a) How many outcomes can there be in this election? A possible outcome would
be 5 votes for the winner, 4 votes for second place and 1 vote for third place.
b) Out of those outcomes, how many ties could there be?
c) What is the probability of the election resulting in a tie?
d) Does increasing the number of voters, decrease the probability of a tie?
- Find the coefficient for the term x^3y^4 from the expression (2x+y)^8?
- For the following problem use Maple V© to find the 8th term. (y^7x^5).
((1/2)x+(2/3)y)^12
- Determine the number of paths from the point (4,2) to the point (7,13) on
an x,y plane.
- The city of Chicago is holding a run. It begins at the corner of 104th and
39th. The organizers are trying to determine the maximum number of entries
they can accept. If each runner must take a unique path to 15th and 30th,
what is the maximum number of runners that can run the specified distance?
(There aren't enough people in Chicago to enter the race. :) )
- There are 12 students sitting side by side on a bleacher row. Three of the
students have on red shirts, seven of the students have on blue shirts, and
two of the students have on black shirts.
a) How many ways can the students be arranged if students with the same color
shirt are considered equivalent?
b) How many ways can the students be arranged so that all of the students
wearing red shirts are side by side (if students with the same color shirt
are considered equivalent)?
- Four (male/female) couples are headed to a Bears/Packers game in Champaign.
Three of the couples are Bears fans. The other couple loves the Packers. In
how many ways can
a.) the fans all sit in a row where couple and team do not matter?
b.) they sit with the Packer fans on the ends (to keep them quiet)?
c.) how many ways can the men sit as a group to the right and the women sit
as a group to the left of the men?
d.) same as part c, but also the Packer couple is the dividing group between
men and women? (So they sit in the middle seats with men on the right and
women on the left).
e.) they be ordered where the Packer fans can't sit directly beside each other?
- There are 3 sizes of square tiles: 2", 3", and 4". Find the
dimensions of a box base (square base) that would accommodate all three tile
sizes (i.e., you could pack it with 2" tiles, or 3" tiles, or 4"
tiles).
- A domino company wants to make a box for their dominoes. They want the box
to be a cube (each edge same length). They also want no extra spaces when
the dominoes are stacked in the box, no matter how you stack them. The size
of a domino is
28 x 14 x 3 mm.
a) What is the smallest sized box that would fit these specifications?
b) How many dominoes would fit in it?
- What number am I? If you add 16 to me, the gcd of 1365 and the new me is
3. The lcm of the new me and 1365 is then 619710.
New Problems: Click here
for a Word document with more problems and true-false items (50 or so).
Answers
- 13+12+11+10+9+8+7+6+5+4+3+2+1= (14)(13)/2 = 91 exchanges
- Disreguard the fact that all students must start with the people in the
same room, but remember to add in their 2nd meeting to check answers afterwards:
18+17+16+15+14+13+12+11+10+9+8+7+6+5+4+3+2+1+6+5+4+3+2+1+4+3+2+1+3+2+1+2+1
=
((19)(18)/2) + ((7)(6)/2) + ((5)(4))/2 + ((4)(3))/2 + ((3)(2))/2 = 211 meetings.
- Combinations with repetitions. C(33, 3) = 5,456 ways.
- Combinations with repetitions. C(12,2) = 66 ways.
- a)
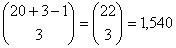
b) 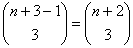
- a) This can be handled like Ex. 1.37 on page 33. a <= b <= c <=
10.
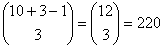
b) Note, because of the tie, one of the dividers can be removed resulting
in two dividers. a <= b = c <= 10. Treat b and c as the same.
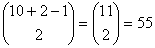
c) 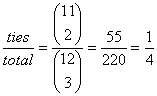
d) Yes, to see why, graph this function where n is the number of voters:
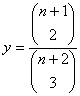
- C(8,3)*(2)^3 = 448.
- 352/243.
- 14!/(11!*3!) = 364 paths
- 98!/(9!*89!) = 1.57 X 10^12 paths
- a) 12!/(3!7!2!) = 7920
b) 10!/(7!2!) = 360
- a) 8! = 40320
b) 2 * 6! * 1 = 1440
c) 4!4! = 576
d) 3! * 1 * 1 * 3! = 36
e) Fix the six Bear fans. Visualize 7 dividers. Choose two for the Packer
fans (keep those Packer fans apart).
C(7, 2) = 21.
- 12" x 12" (the LCM).
- a.) The LCM (28, 14, 3) = 84.
So the box would be (84 x 84 x 84 mm)
b). 84/3 = 28
84/14 = 6
84/28 = 3
3 x 6 x 28 = 504 dominoes
- ab = gcd(a,b) * lcm(a,b)
(x + 16)(1365) = (3)(619710)
1365x + 21840 = 1859130
1365x = 1837290
x = 1346
Click here to go to the quick notes from Wednesday
10/16/2002.
Back to Jim Olsen's
homepage
James R. Olsen, Western Illinois University
E-mail: jr-olsen@wiu.edu
Page last updated:
December 5, 2002
![]()
![]()