Problem:  Your employer manufactures circuit boards in a variety of convex shapes.  The board must be convex so that any two points on it can be joined by a straight segment of wire lying entirely on the surface of the board.  What circuit board shapes can be designed using all 7 pieces of the tangram set?
  Work with a partner using all 7 pieces of a tangram set to design as many convex polygon shapes as you can for circuit boards.
  Use uncooked spaghetti to check that your shapes are convex: Connect any two points on the polygon with a piece of spaghetti.  If the spaghetti that lies between the two points lies entirely within the polygon, it is convex.  If part of the segment of spaghetti between the two points falls outside the shape, it is concave.
  Record your convex shapes by tracing around their borders.  Cut out your convex shapes and sort them by the number of sides they have.
  Make sure all of your shapes are different.  Be ready to discuss the shapes you have found.

Math Topic/Concept:  Comparing polygons: concave, or convex

Materials:  tangrams, 1 set per student,  uncooked spaghetti, scissors

Classroom Use: (Introductory/Developmental)

Classroom use comments*:  Use this activity to discuss strategies to design convex shapes, different ways to check that all were different,  properties of polygons, etc.

Grade:  7-8

Grade Cluster: (MS-Jr.High)

Illinois Goal:  9: Geometry

Standard:  9A3c,  9B3

Applied? (1-4):  2

Source:  Super Source: 7-8, Geometry , Cuisenaire, 1998 ISBN: 1-57452-011-3

Answer:  There are 13 unique convex polygons, using all 7 pieces of a tangram set.

Strategies Listed:  Use a model, use manipulatives, Guess and Check.

Solution:  various

Extensions or related problems*:  Students may explore whether there are more or fewer concave polygons that can be made with a 7-piece tangram set.  They may also extend to using two sets of tangrams.

Intended rubric or assessment method:  Assess: were all polygons convex?  Did students work together to find as many polygons as possible?  Did students sort polygons by number of sides?  Could students describe properties, and any patterns or relationships noted?

Notes*:  Journal writing entries might respond to: “Describe the difference between a convex and concave polygon.  State two methods to determine whether a polygon is concave or convex.

Write-up submitted by:  M.K. Robbins

Problem:  You work for a company that manufactures jigsaw puzzles for the visually impaired.  Your job is to write step-by-step instructions for assembling the puzzles.  The instructions are then translated into Braille for the visually impaired.
· Sit back-to-back with your partner so that you cannot see each other’s work.  Make a puzzle design using 5 to 7 pieces of a tangram set.
· Record your design by tracing the pieces on paper.  This will be your answer key.
· On a second sheet of paper, write step-by-step instructions for placing your tangram pieces into the puzzle you designed.  Be concise, using mathematical terms without drawings.
· Exchange instructions with your partner.  Follow your partner’s instructions to make his design.
· When finished, compare the finished puzzle to the answer key.  Discuss how the designs compare and how the written instructions might be improved.

Extension problem:
 You are promoted at the puzzle factory.  Your new job is to write instructions for the jigsaw machine to cut the frame of the finished puzzle design.  The jigsaw will follow your instructions, moving around the border of your puzzle to make appropriate cuts.
· Sit back-to-back with your partner so that you cannot see each other’s work.  Make a puzzle design using 5 to 7 pieces of a tangram set.
· Make an answer key by tracing the frame or outline of your puzzle on a piece of paper.
· On a second sheet of paper, write the commands you would use to program the jigsaw to cut the frame of your puzzle.  Select one vertex as your starting point.  Use a ruler and protractor as measuring tools to write a series of steps that will generate the path around your design, ending back at the starting point.
· Exchange instructions with your partner.  Follow your partner’s instructions for making his or her puzzle frame.
· When finished, compare to the answer keys, and discuss how the written instructions might be improved.

Math Topic/Concept:   properties of polygons,  Measurement of angles and distances, Writing/communicating mathematical descriptions and instructions

Materials:  1 set of tangrams per student.    Protractor, ruler, pencil and paper

Classroom Use: (Introductory/Developmental/Evaluation)

Grade:  7 - 8

Grade Cluster: (EarlyElem/LateElem/MS-Jr.High/EarlyHS/LateHS)

Illinois Goal:  9 & 7  Geometry and Measurement

Standard:  9B3, 9C3a, 7A3a, 7B3

Applied? (1-4):  3

Source:  Super Source for 7-8 Geometry, Cuisenaire: 1998, ISBN: 1-57452-011-3

Answer:  varies, depending on student design

Strategies Listed:  Make a diagram

Solution:  varies

Extensions or related problems*:  Students might use 3-D solids to build towers and describe them to a partner who then must build a copy of the tower.

Intended rubric or assessment method:  Were the instructions complete, concise, and accurate?  Did instructions include appropriate mathematical language?  Were measurements accurate?

Notes*:    Although the Braille jigsaw puzzle premise may be a bit contrived, technical writing and following technical instructions is a highly applicable skill in daily life.

Write-up submitted by:  M. K. Robbins

Problem:  Four sisters inherited a square plot of lane with twelve peach trees arranged as shown on the diagram below.  How can the plot of land be divided into four sections of equal area so that each section contains three trees and each resulting plot has only square corners?
 

Math Topic/Concept:  Spatial Reasoning

Materials: Tree Plot

Classroom Use: (Introductory)

Grade:  6-8

Grade Cluster: (MS-Jr.High)

Illinois Goal:  9

Standard:  9.B.3

Applied? (1-4): 3

Source: Mathematics Teaching in the Middle School (March 99)

Answer: There is more than one solution.
 

Strategies Listed:  Guess and Check by drawing

Solution:
 

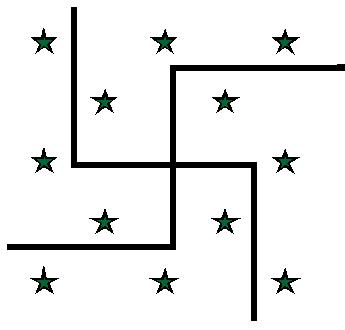
Extensions or related problems*:  Change the number of trees, sisters or the requirement of having a square corner.

Intended rubric or assessment method:  Does their picture meet the criteria?

Write-up submitted by:  Denise Mann and Jenni Robinson

Problem: How many 3-, 4-, 5-, and 6-sided figures to you see below? You get 3 points for each triangle, 4 points for each 4-sided figure, etc.

How many points did you get?
 

Math Topic/Concept:  Spatial and Number Sense

Materials:  Diagram with score sheet

Classroom Use: (Developmental)

Classroom use comments*:  Review the names of the sided figures.

Grade:  6-8

Grade Cluster: (MS-Jr.High)

Illinois Goal:  9

Standard:  9.B.3

Applied? (1-4):  1

Source:  Awesome Math Problems (Grade 6)

Answer:  Greatest possible total is 49 points.

Strategies Listed:  Organized list of figures found.

Solution:  Triangles – 4, Quadrilaterals – 4, Pentagons – 3, and Hexagons – 1.

Intended rubric or assessment method: Students must list all their figures found with letters.

Write-up submitted by:  Denise Mann and Jenni Robinson

Problem:  Place sixteen toothpicks as shown.

Remove four toothpicks to leave four
congruent equilateral triangles.

Math Topic/Concept:  Spatial Reasoning and Properties of  triangles

Materials:  toothpicks

Classroom Use: (Developmental)

Classroom use comments*:  Discuss properties of equilateral triangles.

Grade:  6-8

Grade Cluster: (MS-Jr.High)

Illinois Goal:  9

Standard:  9.B.3

Applied? (1-4):  1

Source:  Teaching Mathematics in the Middle School  May 2000

Answer:  many possible solutions

Strategies Listed:  Act out with toothpicks

Solution:  Remove the two toothpicks straight down the middle, the upper left connected to the middle and the lower right connected to the middle.

Intended rubric or assessment method:  Check student work to see if meets criteria.

Write-up submitted by:  Jenni Robinson and Denise Mann
 
 

James R. Olsen, Western Illinois University
E-mail: jr-olsen@wiu.edu
updated June 27, 2001