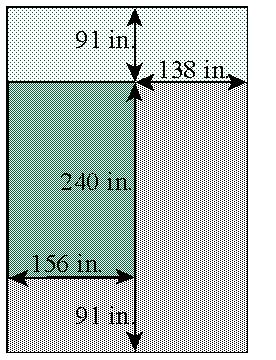
Problem: On Friday, April 7, the levee in Keithsburg, Illinois broke due to high waters.  As a result, Mrs. McClee’s basement was flooded with a large amount of water. As she cleaned the mess and stopped the water from coming in, she wondered how much water was in her basement.  Being very good in math, she remembered that one cubic foot holds 7.48 gallons.  When the water stopped coming in she had 2 inches of water covering the backward L-shaped section in the diagram.  At that time, Mrs. McClee pulled out her trusty 12-gallon shop vac and got to work.

Questions: How many gallons of water (rounded to the nearest whole number) were in the basement?  When Mrs. McClee had finished cleaning up, how many times had she emptied her shop vac?

Math Topic/Concept: Volume and Units of Measure

Materials:  Copy of the picture

Classroom Use: (Developmental)

Classroom use comments*: Review with the students the concept of a cubic foot.

Grade:  5

Grade Cluster: (LateElem)

Illinois Goal: 7 & 8

Standard:  7A2, 8B2

Applied? (1-4):  3

Source:  http://mathforum.com/elempow/print_puzzler.ehtml?puzzle65

Answer:  There were 518.4 gallons (Rounded). She would have to empty the shop vac 44 times.

Strategies Listed: Multiplication and division of whole numbers, finding the area and volume.

Solution:
      Volume is length x width x height. The first volume
       was the small blue area on the left bottom corner. The height is 2
       inches of water. The volume was 156 in. x 91 in. x 2 in. = 28,392
       cubic inches. The second volume was the large blue area on the right
       bottom corner. The length was 240 in. + 91 in. = 331 in. The volume
       was 331 in. x 138 in. x 2 in. = 91,356 cubic inches. The total volume
       of the water was 28,392 cubic in. + 91,356 cubic in. = 119,748 cubic
       inches.

       A cubic foot is 7.48 gallons. A cubic foot is also 12 in. x 12 in. x
       12 in. = 1,728 cubic inches. I figured out the number of gallons per
       cubic inch by dividing 7.48 gallons per cubic foot by 1,728 cubic
       inches per cubic foot to get .0043287 gallons per cubic inch. I
       figured out the gallons in the basement by multiplying 119,748 cubic
       inches x .0043287 gallons per cubic inch = 518 gallons (rounded).
       Could accept 519 or 520 gallons depending on how they rounded.

       I divided the amount of water by the size of the vac. I divided 518.4
       gallons by 12 gallons in the vac to get 43.2 empties of the vac. Mrs.
       McClee could have emptied the vac 43 times and left a little water in
       the vac. I think that Mrs. McClee wouldn’t leave water in the vac, so
       she emptied the vac 44 times.

Other solution methods (if any)*: NA

Extensions or related problems*: The city of Keithsburg’s insurance company has agreed to replace the carpeted area, shown by both the backward L-shape and upside down L-shape on the diagram.  To remove the old carpet and replace it costs $15.44 per square yard.  How much will the bill for the carpet replacement be (not including tax)?

      Mrs. McClee would have to pay $1,034.48. I got that by getting
       the area of the green and blue parts and multiplying by the price. I
       wrote down the areas of the 2 green parts and the 2 blue parts and
       added them up. Area is length times width.
       156 in. x 91 in. = 14,196 square in.
       331 in. x 38 in. = 45,678 square in.
       156 in. x 91 in. = 14,196 square in.
       91 in. x 138 in. = 12,558 square in.
       TOTAL              86,628 square in.
       A square yard is 36 in. x 36 in. = 1,296 square inches. I converted
       the area to square yards by dividing 86,628 square in. by 1,296
       square in. per square yard to get 67 square yards (rounded). I think
       the store would sell whole square yards, not fractions. He would pay
       67 square yards x $15.44 per square yard or $1,034.48.

Intended rubric or assessment method:
Assessment ISAT Mathematics Grade 5 Student-Friendly Rubric
http://www.isbe.state.il.us/isat/rubric5.htm

Write-up submitted by: Carl Carlson – Westmer School

Problem:  Pose this task: Create a map of a campground using specific data provided.*  Establish a grid in order to locate items on the map you create.  (* Teacher can identify 5 general features and then add 2 or 3 varied features for each student.)  Pose 5 general questions which every student can answer regardless of the specific data they will use to create maps, such as:

1. If you stay on the path, how far will you have to walk (with your gear) from the parking lot to the camping area?
2. What is the total distance around the lake if you stay on the hiking trail?
3. What are the coordinates for the location of the ranger’s station?
4. How far would it be to carry a canoe from the rental shed to the closest edge of the lake?
5. What are the coordinates for the location of the concession stand?

After students have drawn their own maps and established grids with appropriate scales (using the length of one unit to represent either 1/8 mile or .2km), they will create 5 tasks for a partner student to accomplish.  For examples, 1. Locate the coordinates of the windmill in the miniature golf course.  2. Measure the distance from the bridge to the swimming pool if you cut through the ball diamond.  3. Draw a bear at (3,6).  4.  Measure the shortest distance across the lake.  5.  Find the lost shoe and tell where to find it.

Math Topic/Concept: algebraic thinking, plotting coordinates on a grid, interpreting data given and translating data to a drawing, interpreting and creating scale

Materials:  white paper, pencils, rulers, grid paper or grids on transparencies, and lists or cards of data

Classroom Use: (Evaluation)

Classroom use comments*:  Prior to this activity, students should have several opportunities to use pre-made grids to locate coordinate points and to add or identify objects within the grids.  They should be aware of how to establish the increments on the vertical and horizontal base lines.  They should know to begin at “ground zero” for each side of the graph or grid.  They also should review and understand the concept of scale.

Grade:  4-5

Grade Cluster: (LateElem)

Illinois Goal:  8

Standard:  8.A.2a and 8B.2

Applied? (1-4):  3

Source:  adapted from several textbooks’ worksheets on grids

Answer:  vary according to teacher’s criteria and on students’ individual interpretation of the data.  Check students’ work for accuracy.

Strategies Listed:  use logical and critical thinking, make a grid, make a map, create reasonable tasks for another student using grid/map, use measurement and scale

Solution:  Students draw maps and create grids using measurement (km or miles as given), estimate and answer class questions, create 5 tasks for other students to use, and do 5 tasks given by another student.

Extensions or related problems*:  Use state maps to plan trips, locate points of interest, or plot new roads or towns.  Use computer program to create map and grid.

Intended rubric or assessment method:  Analytical Scoring Scale (Jim Olsen, WIU)

Write-up submitted by:  Rebecca Cummins (Westmer CUSD 203)
 
 

James R. Olsen, Western Illinois University
E-mail: jr-olsen@wiu.edu
updated Aug. 20, 2001