Title: Band around the World
Problem: The circumference of the Earth is approximately 40,000 kilometers,
and someone has just made a metal band that circles the Earth, touching the
ground at all locations. It is like a big metal belt that goes around the equator.
You come along at night, as a practical joke, and add just 10 meters to its
length (one hundredth of one kilometer !)
It is now one four-millionth longer, and sits magically just above the ground
at all locations
How far has it risen ... could a flea, a rabbit or a man squeeze underneath
it?
Math Topic/Concept: Geometry, circumference, radius.
Materials: Paper/pencil
Classroom Use: (Introductory/Developmental/Evaluation) Developmental
Classroom use comments: This would be a good problem to use after introducing the formulas of circumference and area
Grade: Middle school/high school/whenever circumference and radius are explored.
Grade Cluster: (EarlyElem/LateElem/MS-Jr.High/EarlyHS/LateHS) Probably middle school.
Illinois Goal: 8: Use algebraic and analytical methods to identify and describe patters and relationships in data, solve problems and predict results.
Standard: Use algebraic concepts and procedures to represent and solve problems.
Applied? (1-4): 2
Source: www.niquette.com puzzles with a purpose
Answer: A man.
Strategies Listed: Draw a diagram, apply a formula, subtract, divide
Solution: If the metal band is 40,000 kilometers, then the radius of the earth is 20,000/pi meters. If the metal band is 40,000.01 kilometers(40,000 kilometers + 10 meters), then the radius from the center of the earth to the band is 20,000.005/pi kilometers. That's .005/pi kilometers more, which is roughly 1.6 meters, plenty of room for a man to crawl underneath.
Other solution methods (if any):
Extensions or related problems: Find the amount added to the belt to make the belt float 1 meter above the earth, 10 meters above the earth, etc.
Intended rubric or assessment method:
1 point for correctly setting up the formula.
1 point for calculating the difference properly.
1 point for interpreting the results properly.
Notes (if any): This is very counter intuitive. The way circumference grows relative to radius growth is very different from the way area grows relative to radius growth. One is linear growth and the other is quadratic growth. The large numbers make this more difficult to think about. Also, it should be noted that the original circumference does not matter on this problem. It could have been a basketball!
Write-up submitted by: Megan Orton
Title: Balancing Bowls
Problem: Martha has a balancing scale and finds that a glass and a bowl balance a mug. The bowl alone balances a glass and a plate, and three plates balance two mugs. How many glasses balance a bowl?
Math Topic/Concept: Measuring, Balancing Equations
Materials: pencil and paper
Classroom Use: (Introductory/Developmental/Evaluation)
Classroom use comments: This could be used as a take home problem or an in class problem for a problem solving unit.
Grade: Algebra I, 9th grade
Grade Cluster: (EarlyElem/LateElem/MS-Jr.High/EarlyHS/LateHS)
Illinois Goal: 7.A.4
Standard: Number & Operations and Algebra
Applied? (1-4): Level 1. There are limited real world elements, but it is still mathematically interesting.
Source: Calendar. Mathematics Teacher. v93 n4 p312-16 Apr 2000.
Answer: 5 glasses
Strategies Listed: Use algebra, Make an organized list
Solution:
|
g + b = m
|
2g + 2b = 2m
|
|
g + p = b
|
2g + 2b = 3p
|
|
3p = 2m
|
p = b – g
|
|
?g = b
|
2g + 2b = 3(b-g)
|
|
2g + 2b = 3b – 3g
|
|
|
5g = b
|
5 glasses balances one bowl
Other solution methods (if any): (Using the same givens)
b = g + p
3b = 3g + 3p
3b = 3g + 2m
3b = 3g + 2(g + b)
3b = 3g + 2g + 2b
b = 5g
Extensions or related problems: An author published a book every two years. When the seventh one was published, the sum of the years of publication was 13,804. In what year was the author published?
The size of a computer screen is indicated by the length of its diagonal. Eric’s new fourteen-inch computer screen has twice the area of his old computer screen. If the two screens are similar in shape, what is the size of Eric’s old computer screen?
Intended rubric or assessment method: 10 points total. One point for each equation given in the problem. One point for each step of the algebra necessary to complete the problem. One point for arriving at 5g = b. One point for stating 5 glasses or 5 glasses balance one bowl.
Write-up submitted by: Andrea Gillett
Title: Cube Area
Problem: Three cubes of volume 1, 8, and 27 are glued together at their faces. What is the smallest possible area of the resulting configuration?
Math Topic/Concept: Area and Volume
Materials: Could use cubes as a visual aid.
Classroom Use: Developmental
Classroom use comments: After students have been introduced to the ideas of surface area and volume this problem could be a good thought provoker.
Grade: Algebra/Geometry
Grade Cluster: Early/Late HS
Illinois Goal: 7,9
Standard: 7.A.4b, 9.aB.4
Applied? (1-4): level 2
Source: Mathematics Teacher – Volume 93-No. 1- January 2000
Answer: 72 square units
Strategies Listed: Visualization and finding surface area of each cube
Solution: Cubes with volumes of 1 cubic unit, 8 cubic units, and 27 cubic units have surface areas of 6 square units, 24 square units, and 54 square units, respectively. Before being glued together, the cubes have a total surface area of 84 square units. The surface area of the three cubes glued together is minimized when one face from the smaller cube is glued a face of a larger cube. Modeling this with blocks is very helpful since a picture was provided. Gluing the cubes together in this manner has the effect of “removing” 12 square units of area, resulting in a solid with a surface area of 72 units.
Other solution methods (if any): none that I know of
Extensions or related problems: This could be done with a different shape.
Intended rubric or assessment method: I would give the problem 10 points. 2 for each surface area being right, 2 for the correct construction or drawing of the solid, and 2 for finding the correct answer.
Notes (if any): none
Write-up submitted by: Lisa Wolf
Title: Let’s bake a cake
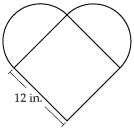
Problem: A baker is making heart-shaped cakes for a wedding. To make a cake look like a heart, he cuts a circular cake in half and attaches the semicircles to a square cake, as shown below.

The baker has to make enough cakes to serve 100 people. He knows that each person will eat approximately 9 square inches of cake.
Complete the following in the Answer Book:
Math Topic/Concept: Area of geometric figures
Materials: calculator, pencil
Classroom Use: (Developmental) This problem is fairly basic in the calculations needed to complete the amount of area in one cake. The difficult part comes into play when the student needs to figure out how many cakes to bake.
Classroom use comments: Students need to think about the number of cakes needed. They often make their mistake when it comes to rounding. They tend to round down based on the answer and forget to put the answer in the context of the question which is how many cakes???? You would not have enough if rounding down.
Grade: 10
Grade Cluster: (EarlyHS)
Illinois Goal: 7.A.4b; 7.A.3b; 7.C.3b
Standard: Geometry , Problem Solving
Applied? (1-4): 3
Source: Maryland State Department of Education Public Release 2002
Answer: The answer would be 4 cakes would be needed if there were 100 people and each slice of cake was 9 square inches.
Strategies Listed:
Students would have to understand concepts of area and calculate the area of the square piece of the cake and the two semicircles of the cake. Then they would have to realize that in order to feed 100 people they would have to calculate how many people could eat one cake.
Solution: Area of the square piece of cake is 144 square inches, semicircles would be 113.04 square inches. The total for the entire cake would be 257.04 square inches per cake. Divide by 9 inches of cake per person and you would get 28.56 people per cake. 100/28.56 gives you approximately 3.5 cakes but you would have to round up and make 4 cakes to feed all the people.
Other solution methods (if any): Some students might calculate an entire circular cake,not the semicircles. Some students might calculate the total number of square inches of cake needed to feed everyone and then divide by the number of square inches per cake.
Extensions or related problems: This type of problem could be used with similar real world problems or shapes of cakes. You could use this type of problem to calculate dimensions of a room and have students fit rectangular beds in the room that have to be a certain amount of feet from each other.
Intended rubric or assessment method:
Level 4 The response indicates application of a reasonable strategy that leads to a correct solution in the context of the problem. The representations are correct. The explanation and/or justification is logically sound, clearly presented, fully developed, supports the solution, and does not contain significant mathematical errors. The response demonstrates a complete understanding and analysis of the problem.
Level 3 The response indicates application of a reasonable strategy that may or may not lead to a correct solution. The representations are essentially correct. The explanation and/or justification is generally well developed, feasible, and supports the solution. The response demonstrates a clear understanding and analysis of the problem.
Level 2 The response indicates an incomplete application of a reasonable strategy that may or may not lead to a correct solution. The representations are fundamentally correct. The explanation and/or justification supports the solution and is plausible, although it may not be well developed or complete. The response demonstrates a conceptual understanding and analysis of the problem.
Level 1 The response indicates little or no application of a reasonable strategy. It may or may not have the correct answer. The representations are incomplete or missing. The explanation and/or justification reveals serious flaws in reasoning. The explanation and/or justification may be incomplete or missing. The response demonstrates a minimal understanding and analysis of the problem.
Level 0 The response is completely incorrect or irrelevant. There may be no response, or the response may state, “I don't know.”
Notes (if any):
Basic problem, but the students have to make the connection of how to calculate the piece that relates to the real world. They also have to make sure they apply the application to the situation at hand and don’t forget that you would not make 3.5 cakes.
Write-up submitted by: Terri Silverman
James R. Olsen, Western Illinois University
E-mail: jr-olsen@wiu.edu
updated:
October 29, 2007