Title: Carl’s Carpet

Problem: Carl’s parents said they would redecorate Carl’s bedroom. Carl wants the floor to be covered with separate sections of red, blue, and white carpet, and he wants the sections arranged so the same color isn’t used in two areas that touch.

Carl’s parents told him to draw a picture of how he wants the carpet to look and to figure out the cheapest way  to use the three colors. They said they’d decide whether they would agree to his plan after they saw it. Carl drew a plan for the carpet on grid paper. Each small square is one square yard.

 

Red = $4.00 per square yard, Blue = $5.00 per square yard, and White = $6. 00 per square yard.

 What colors should be used in each of the six areas A - F?  How much will it cost to carpet the entire room?

Math Topic/Concept: Measurement, Area, Money

Materials: Graph paper

Classroom Use: (Developmental)

Grade: 3-4

Grade Cluster: (LateElem)

Illinois Goal: 7

Standard: 7A2b

Applied? (1-4): 3

Source: Explain It Grade 3-4 by Creative Publications

Answer: Using Car’s plan, $167.00 would be the lowest price for the carpet.

Strategies Listed: Drawing, Paper and pencil

Solution:  Regions A & E have to be the same color and have an area of 18.  Regions C & D have to be the same color and have an area of 13.  Regions B & F have to be the same color and have an area of 5.
Since the red carpeting is the cheapest, it should be used for the largest area (A & E).  Blue is the next cheapest carpet, so C & D should be blue. B and F must be white since the touch both red and blue.

18 sq ft at $4.00 per yd + 13 sq ft at $5.00 per yd + 5 sq ft at $6.00 per yd, or $72.00 + $65.00 + $30.00 = $167.00.

Intended rubric or assessment method: ISAT Rubric

Write-up submitted by: Kathy Erlandson

Problem:  Enrique is going to make cards to label the tables at the science fair. He will cut rectangles that are 4 inches wide and 6 inches long from rectangular poster board that is 2 feet wide and 3 feet long. Enrique is measuring and drawing lines to cut along in order to make the greatest number of cards without wasting any of the poster board. How many cards should he have when he is finished? Explain how you find your answer.

Math Topic/Concept: measuring in inches, converting feet to inches, drawing rectangles

Materials: rulers, paper, pencil

Classroom Use: (Developmental)

Grade: 5-6

Grade Cluster:  (LateElem)

Illinois Goal: 7 & 9

Standard: 7A2a & 9A2

Applied? (1-4): 3

Source: Explain It  Grades5-6 by Creative Publications (ISBN # 0-7622-1598-4)

Answer:  36 cards

Strategies Listed: Draw a picture

Solution: Draw the poster board. Change 2 feet to 24 inches and 3 feet to 36 inches because the cards would be measured in inches. Then I divided the side that was 36 inches long into 6 inch sections to make cards that were 6 inches long. Each card had to be 4 inches wide, and 24 divided by 4 = 6, so 6 cards would fit across. 6 rows of 6 made 36 cards in all.

Intended rubric or assessment method: ISAT rubric

Write-up submitted by:  Jonna Young

Problem: Take an 18-inch cubed box and use it to measure the length, width, and height of your classroom.  Using the measurement in boxes, determine the perimeter, area, and volume of the classroom.

Math Topic/Concept: Measurement, Area, Volume, and Perimeter

Materials: 18-inch square box

Classroom Use: (Developmental)

Classroom use comments*: Perhaps work in groups of 3-5 students

Grade: 4/5

Grade Cluster: (LateElem)

Illinois Goal: 7, 9

Standard: 7A2a, 7B2b, 7C, 9A2a

Applied? (1-4): 2

Source: http://www.isbe.state.il.us/ils/benchmarking/mathactivities.htm#LE

Answer: Will vary according to the measurement of individual classroom.

Strategies Listed: Measurement and the use of formulas for area = length x width, perimeter = sum of all sides of object, and volume = length x width x height.  The extension would use the strategy of converting units of measure (inches to feet) or use of scale in a drawing.

Solution: Take the dimensions of the classroom measured in boxes and use the information in the proper formulas to determine answers.  For example if the length is 25 boxes, width is 30 boxes, and the height is 12 boxes, the area would be 25 x 30 = 750 boxes, the volume would be 25 x 30 x 12 = 9,000 boxes.  The perimeter would be, assuming the room is a rectangle, 25 + 25 + 30 + 30 = 110 boxes.

Other solution methods (if any)*: NA

Extensions or related problems*: Convert the area, perimeter, and volume into total feet.  Another option could be to draw a simple scale drawing of the room based on the information gathered from measuring in boxes.

Intended rubric or assessment method:
Assessment ISAT Mathematics Grade 5 Student-Friendly Rubric
www.isbe.state.il.us/isat/rubric5.htm

Notes*: NA

Write-up submitted by: Carl Carlson – Westmer School

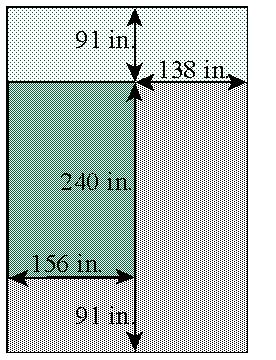
Problem: On Friday, April 7, the levee in Keithsburg, Illinois broke due to high waters.  As a result, Mrs. McClee’s basement was flooded with a large amount of water. As she cleaned the mess and stopped the water from coming in, she wondered how much water was in her basement.  Being very good in math, she remembered that one cubic foot holds 7.48 gallons.  When the water stopped coming in she had 2 inches of water covering the backward L-shaped section in the diagram.  At that time, Mrs. McClee pulled out her trusty 12-gallon shop vac and got to work.

Questions: How many gallons of water (rounded to the nearest whole number) were in the basement?  When Mrs. McClee had finished cleaning up, how many times had she emptied her shop vac?

Math Topic/Concept: Volume and Units of Measure

Materials:  Copy of the picture

Classroom Use: (Developmental)

Classroom use comments*: Review with the students the concept of a cubic foot.

Grade:  5

Grade Cluster: (LateElem)

Illinois Goal: 7 & 8

Standard:  7A2, 8B2

Applied? (1-4):  3

Source:  http://mathforum.com/elempow/print_puzzler.ehtml?puzzle65

Answer:  There were 518.4 gallons (Rounded). She would have to empty the shop vac 44 times.

Strategies Listed: Multiplication and division of whole numbers, finding the area and volume.

Solution:
      Volume is length x width x height. The first volume
       was the small blue area on the left bottom corner. The height is 2
       inches of water. The volume was 156 in. x 91 in. x 2 in. = 28,392
       cubic inches. The second volume was the large blue area on the right
       bottom corner. The length was 240 in. + 91 in. = 331 in. The volume
       was 331 in. x 138 in. x 2 in. = 91,356 cubic inches. The total volume
       of the water was 28,392 cubic in. + 91,356 cubic in. = 119,748 cubic
       inches.

       A cubic foot is 7.48 gallons. A cubic foot is also 12 in. x 12 in. x
       12 in. = 1,728 cubic inches. I figured out the number of gallons per
       cubic inch by dividing 7.48 gallons per cubic foot by 1,728 cubic
       inches per cubic foot to get .0043287 gallons per cubic inch. I
       figured out the gallons in the basement by multiplying 119,748 cubic
       inches x .0043287 gallons per cubic inch = 518 gallons (rounded).
       Could accept 519 or 520 gallons depending on how they rounded.

       I divided the amount of water by the size of the vac. I divided 518.4
       gallons by 12 gallons in the vac to get 43.2 empties of the vac. Mrs.
       McClee could have emptied the vac 43 times and left a little water in
       the vac. I think that Mrs. McClee wouldn’t leave water in the vac, so
       she emptied the vac 44 times.

Other solution methods (if any)*: NA

Extensions or related problems*: The city of Keithsburg’s insurance company has agreed to replace the carpeted area, shown by both the backward L-shape and upside down L-shape on the diagram.  To remove the old carpet and replace it costs $15.44 per square yard.  How much will the bill for the carpet replacement be (not including tax)?

      Mrs. McClee would have to pay $1,034.48. I got that by getting
       the area of the green and blue parts and multiplying by the price. I
       wrote down the areas of the 2 green parts and the 2 blue parts and
       added them up. Area is length times width.
       156 in. x 91 in. = 14,196 square in.
       331 in. x 38 in. = 45,678 square in.
       156 in. x 91 in. = 14,196 square in.
       91 in. x 138 in. = 12,558 square in.
       TOTAL              86,628 square in.
       A square yard is 36 in. x 36 in. = 1,296 square inches. I converted
       the area to square yards by dividing 86,628 square in. by 1,296
       square in. per square yard to get 67 square yards (rounded). I think
       the store would sell whole square yards, not fractions. He would pay
       67 square yards x $15.44 per square yard or $1,034.48.

Intended rubric or assessment method:
Assessment ISAT Mathematics Grade 5 Student-Friendly Rubric
http://www.isbe.state.il.us/isat/rubric5.htm

Write-up submitted by: Carl Carlson – Westmer School

Problem:  Pose this situation:  Ben wants to buy a 75-cent snack from a vending machine at the ball game.  The machine takes only nickels, dimes and quarters. Ben has 7 nickels, 5 dimes, and 2 quarters.  Think about how many ways Ben might be able to pay for the snack with the coins he has.  Record your prediction, plan a strategy, and demonstrate all the different ways  in which Ben can pay for the 75-cent snack. You can use pictures, make a table or write number sentences.  When you think you have found all the ways possible, write down your answer and compare it to your prediction.  Write a response to explain your thinking and what you learned in this exercise.

Math Topic/Concept: estimation and  computation with currency

Materials:  pencil and paper (or math journals) optional: coins for manipulatives

Classroom Use: (Developmental)

Classroom use comments*:  Refresh students’ understanding with a brief demonstration of the exchange of a dime with two nickels, two dimes and a nickel for a quarter, etc.  Remind students to keep in mind all the important facts of the situation (e.g. Ben has 7N, 5D, and 2Q) – what is KNOWN, what is NOT KNOWN, and what are the RESTRICTIONS.

Grade:  4

Grade Cluster: (LateElem)

Illinois Goal: 6 and 7

Standard:  6.C.2a and 7.A.2b

Applied? (1-4):  3

Source:  MPAAC conference discussion

Answer:  There are 8 ways

Strategies Listed:  look for pattern, use logical reasoning, make a table

Solution:  students will most likely develop a T-chart (table) labeled N, D, Q to test and demonstrate the ways.  They should also write an explanation of their thinking processes

Other solution methods (if any)*:  draw pictures of coins or use manipulatives

Extensions or related problems*:    Ask students to find how much change Ben will have left after purchasing his snack.  (62 cents).  Ask students to select another amount to determine how many ways it might be identified; for example, using only nickels and quarters.

Intended rubric or assessment method:  Analytic Scoring Scale (Jim Olsen, WIU)

Write-up submitted by:  Rebecca Cummins  (Westmer CUSD 203)

Problem: The custodians at Westmer High School have been asked to plant new grass seed in the area inside the track.  Before they can determine how much grass seed to buy, they need to find the total area.  What is the area inside the track?  How did you get your answer?
Information (or provide a diagram): A rectangle with semi-circles on the ends.  The rectange is 100 m by 50 m.

Math Topic/Concept: Area, Diameter, and Circumference

Materials: A copy of the picture and possibly a calculator

Classroom Use: (Developmental)

Grade: 5

Grade Cluster: (LateElem)

Illinois Goal: 7, 10

Standard: 7A2a, 10B2d

Applied? (1-4): 4

Source: Exploring Mathematics Practice – Scott Foresman and Company Grade 5 1995

Answer: 5,157 square meters

Strategies Listed: Area of rectangles, area of circles, multiplication, addition

Solution: I started out by recognizing the rectangle in the diagram.  I took the length and multiplied the width to get the area (100m x 50 m = 5,000 square meters).  I then took the diameter of the circle on the left, which also serves as the width of the rectangle, and multiplied by 3.14 (50 x 3.14 = 157 meters squared).  Since that represents the area of the whole circle, I can use that total to represent the area of the two semi-circles attached to the ends of the rectangle.  The total would be 5,000 + 157 = 5, 157 square meters.

Extensions or related problems*: A bag of grass seed at Walmart costs $5.95 (tax included).  One bag of grass seed will cover 20 square meters.  How many bags will need to be purchased?  How much will all the bags of grass seed cost?

I took 5,157 square meters and divided by 20 square meters to figure out how many bags the custodians would need.  The answer for 5,157 ÷ 20 = 257 with a remainder of 17, so they would need to purchase 258 bags to have enough to finish the job.  The cost is figured out by taking 258 bags and multiplying by $5.95.  The answer to 258 x $5.95 = $1,525.10.

Intended rubric or assessment method:
Assessment ISAT Mathematics Grade 5 Student-Friendly Rubric
www.isbe.state.il.us/isat/rubric5.htm

Write-up submitted by: Carl Carlson – Westmer School

Problem:  There are two taxi cab companies in Small Town and they have different rates for determining how much to charge for a ride.
  Speedy Cab Service      $3.00 for the first mile
       $0.50 for each additional mile

Whirlwind Cab Company  $1.00 per mile
With which cab company would you pay less for a 3-mile ride?
Which cab company would be less expensive for a 10-mile ride?
For what distance ride will the two companies charge exactly the same amount?
Explain how you find your answers.
 

Math Topic/Concept:  Number sense, addition, currency

Materials: paper, pencil

Classroom Use: (Developmentalaluation)

Grade:  5

Grade Cluster: (LateElem)

Illinois Goal: 6.B.2 , 7.A. 2b  and 8.D.2

Standard:  6.B.2 ,7.A.2b and 8.D.2

Applied? (1-4):  3

Source:  Explain It!  Grades 5-6 from Creative Publications  ISBN 0-7622-1598-4

Answer: Whirlwind cab would be less expensive for a 3-mile ride.  They would charge $3.00, while the same distance would cost $4.00 with Speedy Cab.
For a 10-mile ride, it would be less expensive to use Speedy Cab.  They would charge $7.50 rather than the $10.00 you would be charged by Whirlwind.

Strategies Listed: While it is a more tedious way to find the comparative rates for the first 10 miles, making a chart as done in Solution 1 makes it easy to compare the rates for any distance quickly.  All students should understand this approach
 
 

Solutions:
Solution 1: You can make a chart showing what the two cab companies would charge
for each distance up to ten miles.  The chart shows that Whirlwind Cab Company is less expensive for traveling distances less than 5 miles, and Speedy Cab is less expensive for distances of more than 5 miles.  They are the same price for exactly 5 miles.

Other solution methods (if any)*:  Solution 2:  Since Speedy Cab Company charges $0.50 for each mile, except for the first mile, which is 3 dollars, their charge is $3.00 + $0.50 x the total miles minus 1.  For Whirlwind Cab, the charge is $1 x the number of miles.  Speedy Cab costs less for a 3-mile ride, but they charge more for a 10-mile ride.
For a 3-mile ride:
Speedy Cab = $3+ ($0.50x{3-1}) = $3+$1=$4
Whirlwind Cab = $3.00
For a 10-mile ride:
Speedy Cab = $3.00 + ($0.50 x{10-1})= $3+$4.50 =$9.00
Whirlwind Cab = $10.00
If there is a place where the charge is the same for both companies, it should be between 3 miles and 10 miles.  By checking different distances, you find that at 5 miles they charge the same rate- $5.00.

Intended rubric or assessment method:  Grade 5 "Student-Friendly" Mathematics Scoring Rubric found at http://www.isbe.state.il.us/isat/rubric5.htm

Write-up submitted by:  Ann Hulsizer , 5th Grade, Monmouth

Problem: Aiesha earns $15 a day babysitting, and Yvonne earns $8 a day looking after neighbors’ pets. After how many days has Aiesha earned $42 more than Yvonne?

Math Topic/Concept:  money, addition , subtraction

Materials: paper and pencil

Classroom Use: (Developmental)

Grade: 5

Grade Cluster: (LateElem)

Illinois Goal: 7

Standard:  7A2

Applied? (1-4): 2

Source:  Middle Grades Math – Tools for Success, Prentice Hall (ISBN# 0-13-427709-0)

Answer:  6 days

Strategies Listed:  Make a table

Solution: Make a table that shows for each day Aiesha works, she makes $15 more. This pattern needs to be extended. The table must also show Yvonne making $8 more each day she works. The table needs to be extended until the 2 amounts can be subtracted and $42 the answer. Then count the number of days it took.

 Day 1 Day 2 Day 3 Day 4 Day 5 Day 6
Aiesha $15 $30 $45 $60 $75 $90
Yvonne $8 $16 $24 $32 $40 $48

Intended rubric or assessment method: ISAT rubric

Write-up submitted by:  Jonna Young

Problem: Find the circumference of the circular object.  How did you get your answer?
Radius measured 12.5 inches
 
 
 

Math Topic/Concept: Radius, Diameter, and Circumference

Materials: Copy of the picture of the object and calculators are optional

Classroom Use: (Evaluation)

Classroom use comments*: Review with the class that pi = 3.14

Grade: 5

Grade Cluster: (LateElem)

Illinois Goal: 7

Standard: 7.A.2a

Applied? (1-4): 2

Source: Exploring Mathematics Practice – Scott Foresman and Company

Answer: 78.5 inches

Strategies Listed: Multiplication, Addition, Finding the diameter, Use of Pi

Solution: Since a radius is half of a diameter I took 12.5 x 2 = 25.  To find the circumference I took the diameter of 25 inches and x by pi (3.14) = 78.5 inches.

Intended rubric or assessment method: Assessment ISAT Mathematics Grade 5 Student-Friendly Rubric
www.isbe.state.il.us/isat/rubric5.htm

Write-up submitted by: Carl Carlson – Westmer School

Problem: Katie's mom said that each time Katie didn’t have her daily chore done by supper time, $0.10 would be subtracted from her allowance of $2.25 per week.  At the end of the week, Katie received $1.85 for her allowance.  How many times was she late doing her chore?

Math Topic/Concept:  Number sense, addition, subtraction, and currency

Materials:  Paper, pencil

Classroom Use: (Introductory)

Classroom use comments*:  Students can work alone and then compare answers with a partner.

Grade:  5

Grade Cluster: (LateElem)

Illinois Goal: 7

Standard:  7.A.2b

Applied? (1-4):  3

Source: Ten Minute Math Mind Stretchers  by Laurie Steding    ISBN 0-590-86563-3

Answer: 4 times

Strategies Listed:  Possible strategies include:  Count up by dimes from $1.85 to $2.25.
You could also write an equation subtracting $1.85 from $2.25.  Then finding the number of dimes in the solution determine the number of times Katie was late doing her chore.

Solution:  Counting up by dimes:  $1.85, $1.95, $2.05, $2.15, $2.25, so the answer is four times.

Other solution methods (if any)*: Or in writing the equation, $2.25-$1.85=$0.40, to find the amount subtracted, then determine the number of dimes in $0.40 is 4 dimes or 4 times Katie was late in doing her chore.

Intended rubric or assessment method:  Informal Observation

Write-up submitted by:  Ann Hulsizer, 5th grade, Monmouth

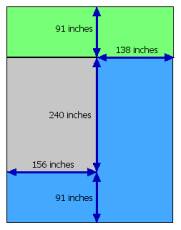
Problem: On Friday, April 7, the levee in Keithsburg, Illinois broke due to high waters.  As a result, Mrs. McClee’s basement was flooded with a large amount of water. As she cleaned the mess and stopped the water from coming in, she wondered how much water was in her basement.  Being very good in math, she remembered that one cubic foot holds 7.48 gallons.  When the water stopped coming in she had 2 inches of water covering the backward L-shaped section in the diagram.  At that time, Mrs. McClee pulled out her trusty 12-gallon shop vac and got to work..
Question: How many gallons of water were in the basement?  When Mrs. McClee had finished cleaning up, how many times had she emptied her shop vac?

Materials:  Copy of the picture

Classroom Use: (Introductory/Developmental/Evaluation)

Grade:  5

Grade Cluster: (EarlyElem/LateElem/MS-Jr.High/EarlyHS/LateHS)

Illinois Goal: 7 & 8

Standard:  7A2, 8B2

Applied? (1-4):  3

Source:  http://mathforum.com/elempow/print_puzzler.ehtml?puzzle65

Answer:  There were 518.4 gallons(Rounded). She would have to empty the shop vac 44 times.  Extension answer: Cost would be $1,034.48.

Strategies Listed: Use a diagram

Solution:
      Volume is length x width x height. The first volume was the small blue area on the left bottom corner. The height is 2 inches of water. The volume was 156 in. x 91 in. x 2 in. = 28,392 cubic inches. The second volume was the large blue area on the right bottom corner. The length was 240 in. + 91 in. = 331 in. The volume was 331 in. x 138 in. x 2 in. = 91,356 cubic inches. The total volume of the water was 28,392 cubic in. + 91,356 cubic in. = 119,748 cubic inches.
       A cubic foot is 7.48 gallons. A cubic foot is also 12 in. x 12 in. x 12 in. = 1,728 cubic inches. I figured out the number of gallons per cubic inch by dividing 7.48 gallons per cubic foot by 1,728 cubic inches per cubic foot to get .0043287 gallons per cubic inch. I figured out the gallons in the basement by multiplying 119,748 cubic inches x .0043287 gallons per cubic inch = 518.4 gallons (rounded).
       I divided the amount of water by the size of the vac. I divided 518.4 gallons by 12 gallons in the vac to get 43.2 empties of the vac. Mr. Basden could have emptied the vac 43 times and left a little water in the vac. I think that Mr. Basden wouldn’t leave water in the vac, so he emptied the vac 44 times.
       Bonus: Mr. Basden would have to pay $1,034.48. I got that by getting the area of the green and blue parts and multiplying by the price. I wrote down the areas of the 2 green parts and the 2 blue parts and added them up. Area is length times width. 156 in. x 91 in. = 14,196 square in. 331 in. x 38 in. = 45,678 square in. 156 in. x 91 in. = 14,196 square in. 91 in. x 138 in. = 12,558 square in.
       TOTAL              86,628 square in.
       A square yard is 36 in. x 36 in. = 1,296 square inches. I converted the area to square yards by dividing 86,628 square in. by 1,296 square in. per square yard to get 67 square yards (rounded). I think the store would sell whole square yards, not fractions. He would pay 67 square yards x $15.44 per square yard or $1,034.48.

Extensions or related problems*: The city of Keithsburg’s insurance company has agreed to replace the carpeted area, shown by both the backward L-shape and upside down L-shape on the diagram.  To remove the old carpet and replace it costs $15.44 per square yard.  How much will the bill for the carpet replacement be (not including tax)?

Intended rubric or assessment method:
Assessment ISAT Mathematics Grade 5 Student-Friendly Rubric
http://www.isbe.state.il.us/isat/rubric5.htm

Write-up submitted by: Carl Carlson – Westmer School

Problem:  Pose this question:  “How would you measure a puddle?”  Discuss all the kinds of measurements they might be able to use, then brainstorm some ideas about how to measure.  Ask students to make estimates for each kind of measure they have suggested.  (How deep?  How cold?  What is the area?  How long to run around it?  How long would it be if it were a creek instead? )

Math Topic/Concept: measurement (length, weight, volume, time, temperature, etc. according to the generated suggestions)

Materials: have available a great variety of tools for measuring, such as: yarn, meter and yard sticks, rulers, scales, cups, clock with second hand or stopwatch, paperclips, thermometers, etc.  Also provide pencil and paper, and A PUDDLE!  (Optional:  create a classroom puddle by pouring water onto black plastic that is molded into a box of sand.)

Classroom Use: (Developmental)

Classroom use comments*: Review customary and metric units prior to this activity or during the introductory discussion.

Grade:  4

Grade Cluster: (LateElem)

Illinois Goal: 7

Standard:  7.A.2a, 7.B.2a, 7.B.2b

Applied? (1-4):  3

Source:  Creative Publications, “Puddle Questions” Investigation 1  (1994)

Answer:  various, according to choices made.  Check students’ work for accuracy.

Strategies Listed: logical and critical thinking, estimation, computation, measurement, conversion (within and/or between metric and customary)

Solution:  Students consider different ways to measure and select appropriate tools.  They work with partners to manipulate the measuring tools and to double check readings for accuracy.  They record estimates and actual measurements, label units appropriately, and convert within and/or between customary and metric units.  You may  want students to measure in both systems to begin developing a sense of reasonableness in comparison.

Extensions or related problems*: Apply to measuring liquid in a wading pool, a bath tub, a swimming pool, and other containers.  Apply strategies to estimating and measuring even larger bodies of liquid.  What about the water tower?  What about grain in the silo?

Intended rubric or assessment method:  Analytical Scoring Scale (Jim Olsen, WIU)

Write-up submitted by: Rebecca Cummins (Westmer CUSD 203)
 
 

James R. Olsen, Western Illinois University
E-mail: jr-olsen@wiu.edu
updated June 27, 2001