Title: Darts, Anyone?

Problem:
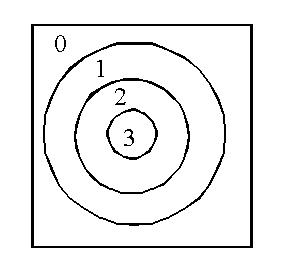
Ted and Kate were making a dart game for their children.  They wanted to have three rings marked with number values. Ted made a board like the one below. When three darts are thrown, what is the lowest score possible? How many different point totals are possible using three darts?
Kate didn’t like this dart board because it permitted only ten different totals for points. That is, using three darts a person could score 0, 1, 2, 3, 4, 5, 6, 7, 8, or 9 points. Show how each total can be obtained with three darts. Kate wondered whether it was possible to label the rings so that a player could reach a higher score with three darts. She wondered whether all the number from 0 to 10 — or even higher — were possible
What suggestions would you give for labeling the rings?

Math Topic/Concept:  Computation, Reasoning

Materials:  Copies of Dart Board; Recording Sheet

Classroom Use: (Developmental/Evaluation)

Classroom use comments*:  This is a good problem for assessing arithmetic review, reasoning, and problem solving.  You might need to make sure that the students understand the problem.  Encourage students to make a systematic listing of the numbers they are choosing.

Grade:  5

Grade Cluster: (LateElem)

Illinois Goal: Goal 6

Standard: 6C1a

Applied? (1-4):  2

Source: Melfried Olson, "Dart's, Anyone",  Teaching Children Mathematics, Volume 5, Number 9, Pages 532- 533.  Solutions in Volume 6, Number 8, Pages 513 - 515.

Answer:  Ten arrangements that produce “better” dart boards are:  (0, 1, 2, 4), (0, 1, 2, 5), (0, 1, 2, 6), (0, 1, 3, 4), (0, 1, 3, 5), (0, 1, 3, 6), (0, 1, 3, 7), (0, 1, 3, 8), )0, 1, 4, 5), and (0, 1, 4, 6).  The choice (0, 1, 4, 6) allows the numbers from 0 – 14 to be obtained.  This is the best choice to attain the longest string of numbers starting at zero.

Strategies Listed:  Make a list, logical reasoning, guess and check

Solution:  After some work with the problem, students should realize that each board must contain a 0 and a 1.  At this point, they can try to list all options that use 0, 1, and 2; 0, 1, and 3; and  0, 1, and 4.

Extensions or related problems*:  Bowl-a-Fact from Measuring Up-Prototypes for Mathematics Assessment, Mathematical Sciences Education Board, National Research Council, National Academy Press, 1993.

Write-up submitted by:  Melfried Olson
 
 
 

Darts Anyone?
Recording Sheet

Four Numbers Used Values That can be obtained the numbers chosen?
0, 1, 2, 3 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,10, 11, 12, 13, 14, 15, 16, 17, 18, __, __, __, __, __
__, __, __. __ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,10, 11, 12, 13, 14, 15, 16, 17, 18, __, __, __, __, __
__, __, __. __ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,10, 11, 12, 13, 14, 15, 16, 17, 18, __, __, __, __, __
__, __, __. __ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,10, 11, 12, 13, 14, 15, 16, 17, 18, __, __, __, __, __
__, __, __. __ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,10, 11, 12, 13, 14, 15, 16, 17, 18, __, __, __, __, __
__, __, __. __ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,10, 11, 12, 13, 14, 15, 16, 17, 18, __, __, __, __, __
__, __, __. __ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,10, 11, 12, 13, 14, 15, 16, 17, 18, __, __, __, __, __
__, __, __. __ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,10, 11, 12, 13, 14, 15, 16, 17, 18, __, __, __, __, __
__, __, __. __ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,10, 11, 12, 13, 14, 15, 16, 17, 18, __, __, __, __, __
__, __, __. __ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,10, 11, 12, 13, 14, 15, 16, 17, 18, __, __, __, __, __
__, __, __. __ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,10, 11, 12, 13, 14, 15, 16, 17, 18, __, __, __, __, __
__, __, __. __ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,10, 11, 12, 13, 14, 15, 16, 17, 18, __, __, __, __, __
__, __, __. __ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,10, 11, 12, 13, 14, 15, 16, 17, 18, __, __, __, __, __
__, __, __. __ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,10, 11, 12, 13, 14, 15, 16, 17, 18, __, __, __, __, __
__, __, __. __ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,10, 11, 12, 13, 14, 15, 16, 17, 18, __, __, __, __, __
__, __, __. __ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,10, 11, 12, 13, 14, 15, 16, 17, 18, __, __, __, __, __

Problem: WANTED: Lightning Bugs and Ladybugs. I will pay 3¢ for each lightning bug, and 5¢ for each ladybug. Professor Reedy

Nancy and Ann saw the professor’s ad, so they brought a sack of 10  bugs to her.  The Professor looked at the bugs and then gave the girls 38¢.  How many of the bugs were lightning bugs and how many were ladybugs?

Math Topic/Concept: money, algebraic thinking, working with variables

Materials: pencils, paper

Classroom Use: (Developmental)

Grade: Third

Grade Cluster: (EarlyElem)

Illinois Goal: 6, 10

Standard: 6.B.1, 6.C.1a, 10.A.1a

Applied? (1-4): 2

Source: The Problem Solver 3, Creative Publications

Answer: 6 lightning bugs, 4 ladybugs

Strategies Listed: Make and organized list

Solution: Ask the students the following questions.
   How many columns are there in the list?
   What are you going to keep track of in your first two columns?
   What are you going to keep track of in the second two columns?
   Finish filling in your list up to 9 lightning bugs and 9 ladybugs.
   Can you find the sums that add up to Professor Reedy”s total?
   Can you find more than one?
Lightning Bugs  Money   Ladybugs  Money
          1           3¢           1            5¢
          2           6¢           2            10¢
          3           9¢           3            15¢
          4           12¢         4 *          20¢ *
          5           15¢         5             25¢
          6 *        18¢ *       6            30¢
 
 
 

Extensions or related problems*:  The next day Nancy and Ann brought 9 bugs to the professor and were paid 39¢.  How many lightning bugs and ladybugs did they sell?

Write-up submitted by: Beth Reedy, third grade, Harding Elementary, Monmouth, Illinois

Problem: Hulsizer Pond has many crayfish and mud turtles who  are there for an egg-laying contest.  Beth Beaver says  she doesn’t know how many crayfish and turtles there are, but she counted 76 legs in all.  Crayfish have 10 legs and turtles each have 4 legs.  How many crayfish and turtles could there be in Hulsizer Pond.

Math Topic/Concept:  Algebraic thinking, working with variables

Materials: paper and pencil

Classroom Use: (Developmental)

Grade: Third

Grade Cluster: (EarlyElem)

Illinois Goal: 6.

Standard: 6.B.1, 6.C.1a

Applied? (1-4): 2

Source: The Problem Solver 3, 1987 Creative Publications

Answer:  6 crayfish & 4 turtles       or          2 crayfish & 14 turtles
      4 crayfish & 9 turtles

Strategies Listed: Guess and Check     Make a Chart

Solution: Make a guess then multiply the number of animals times the number of legs.  Then add the two numbers together and ask yourself these questions.  Was it too low?  Was it too high?

Other solution methods (if any)*:  Make a chart  with 1 crayfish or 1 turtle at the top and progressive increase the numbers until you achieve the correct answer.

Extensions or related problems*:  The next day Beth counted 84 legs.  How many crayfish and turtles could there have been in Hulsizer Pond?

Intended rubric or assessment method: Informal assessment

Write-up submitted by: Beth Reedy, Third Grade, Harding Elementary, Monmouth, Illinois

James R. Olsen, Western Illinois University
E-mail: jr-olsen@wiu.edu
updated Aug. 15, 2001