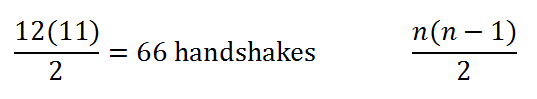
Common Core standard A-SSE is (page 64) Algebra - Seeing Structure in Expressions. Excerpts:
1. Interpret expressions that represent a quantity in terms of its context.★ a. Interpret parts of an expression, such as terms, factors, and coefficients.
3. Choose and produce an equivalent form of an expression to reveal and explain properties of the quantity represented by the expression.★
By Jim Olsen, JR-Olsen@wiu.edu, Western Illinois University. This webpage created for my ICTM presentation on October 18, 2014 (session #99)
Return to Jim Olsen's Homepage. Return to the Common Core Math Standards: Information, Links, and Resources page.